Mathematik ist eine ganz besondere Disziplin, denn diese ist im Gegensatz zu vielen anderen Fächern streng hierarchisch aufgebaut, sozusagen Stufe für Stufe. Einige Kinder haben bereits im vorschulischen Einstieg in die Welt der Zahlen große Probleme, die sich dann auch auf die Grundschulmathematik übertragen, sodass sich auch im weiteren Verlauf des mathematischen Lernens Verständnislücken und Fehlinterpretationen immer weiter verfestigen.
Kleiner Einschub an dieser Stelle: bei Fächern wie der Biologie z. B., kann man vieles über den Frosch lernen auch wenn man nicht weiß, dass dieser von der Schlange gefressen wird. Doch zurück zu den Entwicklungsschritten menschlicher Rechenfähigkeiten, zur „Mathematik von Null an“, sozusagen. Als Grundlage für das weitere Verständnis dient uns das wissenschaftlich fundierten Entwicklungsmodells der Professorin Kristin Krajewski, die den mathematischen Kompetenzerwerbs (Zahl-Größen-Kompetenzen) in drei verschiedenen Stufen skizziert, die alle Kinder von der Geburt bis ins anfängliche Grundschulalter nacheinander durchlaufen.
Ziffern und Zahlwörter ohne Mengen-/Größenbezug
Die Stufe 1 bezieht sich dabei auf zwei verschiedene basale Fähigkeiten, nämlich einerseits die bloße, aber ungenaue Unterscheidung von Mengen bzw. Größen; das können beispielsweise Flächen, Volumen oder Ausdehnungen sein, die Kleinkind different wahrnehmen kann. So wird ein großer Tisch oder Luftballon demnach als größer identifiziert, als ein kleiner. Nachgewiesen wurde diese angeborene Fähigkeit übrigens auch bei bestimmten Tieren, wie Affen oder Bienen. Andererseits rechnet Krajewski dieser Ebene auch die verbal-sprachliche Fähigkeit kleiner Kinder zu, die Namen, also die Zahlwörter zu benennen, wie z. B. eins, drei oder fünf usw.; diese werden beispielsweise durch Gespräche der Eltern aufgenommen und bei hochfrequenter Wiederholung dann als Wortform im mentalen (phonologischen) Lexikon abgespeichert. Wichtig ist, dass an dieser Stelle keinerlei echtes und damit kardinales Zahlenverständnis vorliegt, sodass die Kinder die Wörter nur unreflektiert „nachplappern“ und keine konkrete Menge mit einem Zahlwort verbinden. Abgeschlossen wird die Stufe 1 durch das mehr oder weniger korrekte Aneinanderreihen der Zahlwörter bis hin zur Wiedergabe einer exakten Zahlenfolge. Dieses fehlerfreie „Aufzählen“ von eins, zwei, drei, vier fünf usw., vergleichbar mit dem korrekten Aufsagen der Buchstaben des Alphabets – suggeriert beim Rezipienten das Wissen des Kindes, dass nach der Eins die Zwei und danach die Drei kommt usw.; in Wirklichkeit ist das scheinbar korrekte Aufsagen aber nichts weiter, als das Aufsagen einer auswendig gelernten, aber inhaltlich (numerisch) nicht verstandenen Strophe eines Liedes.
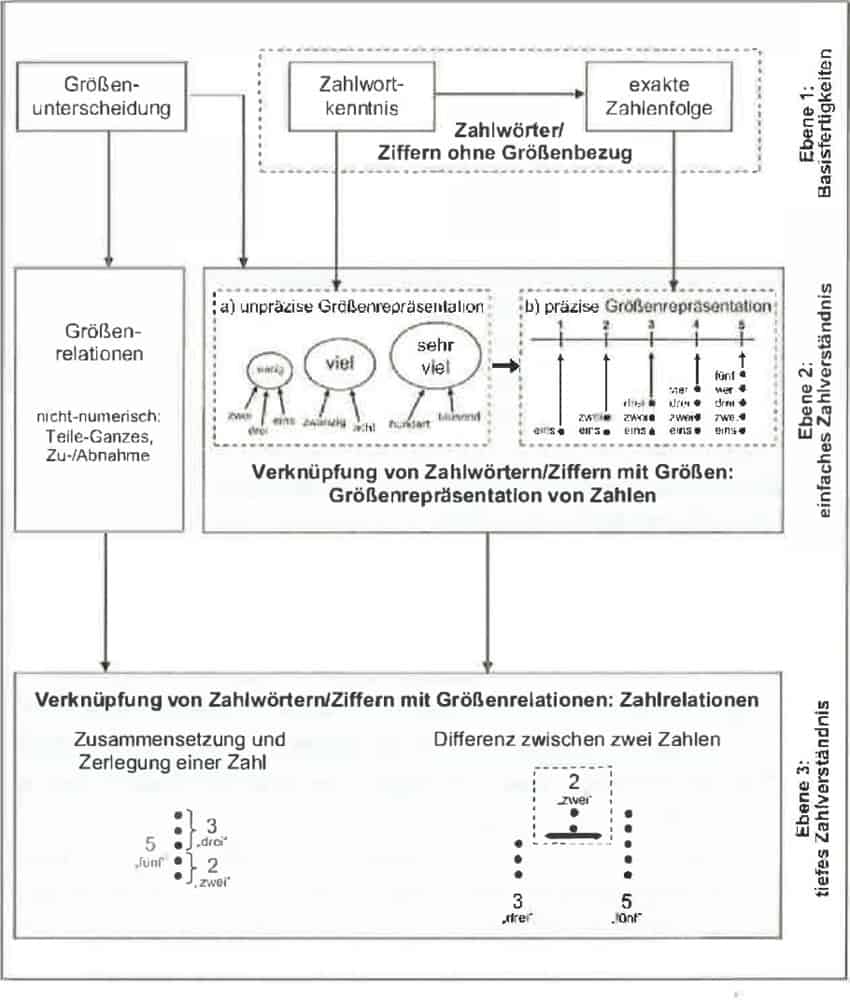
Verknüpfung von Ziffern und Zahlwörtern mit Mengen/ Größen
Die zweite Stufe oder Ebene der kindlichen Entwicklung mathematischer Kompetenzen beginnt mit der Einsicht der Kinder – und Krajewski spricht hier von einem Meilenstein – , dass die o. g. Zahlwörter Mengen bzw. Größen repräsentieren: so wird der „Eins“, „Zwei“ oder „Drei“ zunächst eine kleine Menge (an Dingen) zugeordnet, wohingegen „zehn“ oder „zwanzig“ schon als große Menge abstrahiert wird und „hundert“ oder „tausend“ dann als sehr große. Kinder lernen, dass es länger dauert, bis zur Zehn zu zählen, als bis Drei und vermuten deshalb, dass Zehn folglich größer sein muss. Wie viele Dinge sich konkret hinter dem Zahlwort „Acht“ oder „Zehn“ verbergen, ist jedoch in diesem frühen Stadium der zweiten Stufe immer noch nicht entwickelt. Im unmittelbaren Anschluss an die „unpräzisen Repräsentationen von Größen und Mengen“ gewinnen die Kinder jedoch zunehmend ein kardinales und damit präzises Größenverständnis: dem Zahlwort „Fünf“ werden nun exakt fünf Dinge bzw. Elemente zugeordnet bzw. mit diesem verknüpft. Sie erkennen auch, dass die Zahlwortreihe mit jedem neu hinzukommenden Zahlwort immer um eins zunimmt („n+1-Strategie“). Oder anders ausgedrückt: Mengen werden konkretisiert und durch Symbole (1, 2, 3, 4 usw.) repräsentiert bzw. dargestellt. Mittels dieser Verknüpfung zwischen Zahlwörtern bzw. den entsprechenden Ziffern einerseits und von beliebig auszählbaren Mengen (z. B. 5 Legosteinen) andererseits entsteht ein einfaches Zahlverständnis und es gelingt eine präzise Größenrepräsentation von Zahlen mit den entsprechenden Objekten (eins ▲, zwei ▲▲, drei ▲▲▲…). Gleichzeitig wird ihnen bewusst, dass eine gegebene Menge sich dann vergrößert, wenn ihr einzelne Teile hinzugegeben werden – gleiches gilt auch für den umgekehrten Fall und stellt somit den Vorläufer zur Addition und Subtraktion dar. Auch sehen sie, dass sich eine beliebige Menge in kleinere Teilmengen zerlegen und auch wieder zusammensetzen lässt („Zerlege bitte den Haufen Gummibärchen in drei ungefähr gleich große Teile“). Hier spricht man dann vom Teile-Ganzes-Konzept.
Verknüpfung von Zahlwörtern und Ziffern mit Mengen- und Größenbeziehungen
Die letzte Stufe im Krajewski-Modell setzt nun genau an dieser Nahtstelle an: hierbei geht es nun nicht mehr um die reine Größenrepräsentation von Zahlen, sondern um sog. Zahlenrelationen bzw. die Einsicht in die Zahlbeziehungen, dass sich Zahlen exakt zerlegen und wieder zusammenfügen lassen (6 Pferde lassen sich aufteilen in 4 große und 2 kleine) und dass man präzise Differenzen zwischen zwei Zahlen/Mengen bestimmen kann (z. B. 5 sind 2 mehr als 3). Immer wieder gibt es Kinder, die bei entsprechenden Vergleichsaufgaben (ich habe 5 Gummibärchen und du hast 3, wie viele habe ich mehr als du) Schwierigkeiten haben und in ihrer individuellen Entwicklung diesen Meilenstein noch nicht sichern konnten.
Praktischer Bezug des Modells
In unserer Arbeit mit rechenschwachen Kindern aus den unterschiedlichsten Grundschulkassen konnten wir feststellen, dass einige der Kinder Probleme hatten, Zahlen korrekt zu lesen oder zu schreiben bzw. mit der exakten Verortung dieser auf dem Zahlenstrahl. Auch haben diese oftmals Probleme, Mengen zu schätzen oder zu vergleichen, abgesehen von unzulänglichen Zählstrategien und Probleme beim schnellen Zählen. All dies weist darauf hin, dass bei diesen Kindern grundlegende Defizite des mathematischen Verständnisses im Sinne der Stufen 1 und 2 des Modells der Zahl-Größen-Verknüpfung nach Krajewski bereits weit vor Eintritt in das Schulleben vorliegen und dadurch ein erfolgreicher Erwerb schulmathematischer Kompetenzen stark gefährdet ist. Die Schere zwischen den Kindern, die mit relativ stabilen Zählfertigkeiten und Mengenabstraktionen ausgestattet sind und derer, bei denen diese Grundlagen sehr schwach ausgeprägt sind, ist demnach bereits lange vor dem eigentlichen Einschulungstermin weit geöffnet.
Frühe Vorhersage mathematischer Kompetenzen
Die genaue Beschreibung der 3 Stufen nach Krajewski sollte deutlich machen, dass es bereits in diesem frühen Stadium und banalen Bereich der Mathematik zu unendlich vielen Missverständnissen und Fehlinterpretationen kommen kann, so dass das „Gebäude“ der Mathematik sehr schnell in eine Schieflage bzw. zum kompletten Einsturz kommen kann, da eine stabile, tragende Basis einfach nicht vorhanden ist. Und gerade diese unteren Ebenen, auf die die gesamte Grundschulmathematik aufbaut, kann für einige Kinder, deren mentale Entwicklung noch nicht so weit fortgeschritten ist, zu einem großem Problem werden, da die Zeit, die Kinder in der Klasse 1 und 2 dann haben, viel zu kurz ist und die Fülle an Stoff und der dadurch bedingten schnellen Abstraktion von der Menge zur Zahl nicht verstanden werden kann. Gleiches gilt auch für Kinder, die über einen längeren Zeitraum krank gewesen sind oder über Wahrnehmungs- bzw. Aufmerksamkeitsschwächen verfügen.
Im Beitrag verwendete Fachliteratur
Schneider, W. / Küspert, P. / Krajewski, K.: (2016): Die Entwicklung mathematischer Kompetenzen, 2. erweiterte Auflage, Paderborn: Ferdinand Schöningh



